Gossip算法是分布式网络系统中的重要算法，在分布式计算网络、传感器网络、P2P服务网络和社会网络等领域都有着重要的理论与应用价值。基于gossip原理的协议已经成为现代分布式系统的一类标准解决方式；Gossip算法也是社会网络信息传递和观点演化的一个基本模型。该算法的渐进收敛性以及收敛效率一直是这方面的研究热点。该算法理论模型由图灵奖得主Karp 与其合作者在2000年提出，并给出渐近收敛性证明。众多研究者，包括麻省理工学院Shah教授，加州理工学院Murray院士，斯坦福大学Boyd 教授，都继续深入研究了gossip算法的渐近收敛性。

对于计算机网络和网络控制中的gossip算法，现在已经有了深刻的理论认识。但是渐近算法在有限时间内只能给出近似结果，只有有限时间收敛算法才可以给出精确结果。那么一个重要的问题是，确定性有限时间收敛的对称gossip算法是否存在？如果存在，该算法的计算复杂度是多少？

最近，李博与澳大利亚国立大学的石国栋博士，瑞典KTH的Mikael Johansson教授，Karl Henrik Johansson教授（IEEE Fellow）合作构造性的给出了确定性gossip有限时间收敛算法。他们证明了一个由n个结点组成的网络上可能存在精确有限时间收敛gossip算法的充分必要条件是n是 2 的幂次。如果n不是2的幂次，则对于几乎所有的初值，都不存在有限收敛的gossip算法。根据Borel-Cantelli引理，在满足有限时间收敛的条件下，随机gossip算法以概率1有限时间收敛。该结果刻画了基于gossip协议的计算机网络应用的性能极限。利用算法复杂性理论，他们进一步证明了该算法是理论上可能存在的最快的算法。

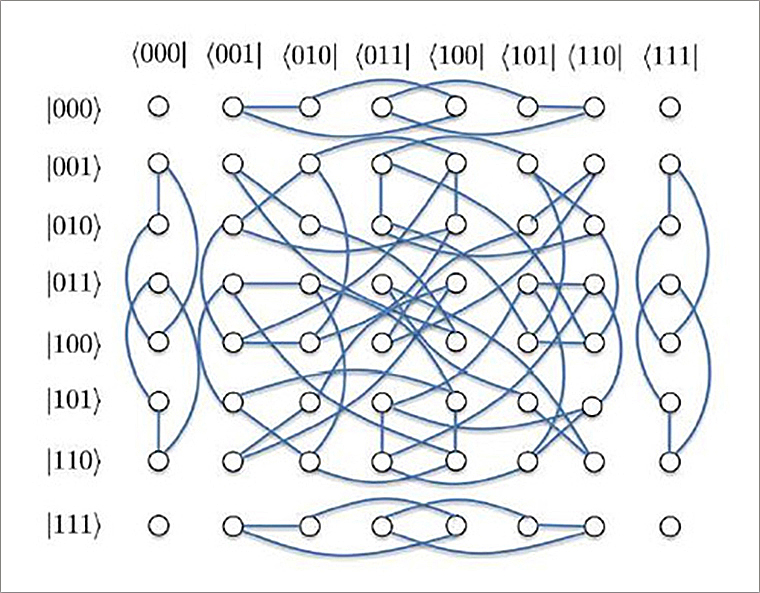
早在2013年意大利学者Mazzarella 等人提出了量子gossip算法并证明了在相当广泛的条件下，该算法渐进收敛。李博与合作者发现，这一n量子比特的gossip算法等价于一个总共有 22n个结点的分区块的并行计算的经典对称gossip网络。这些连通的网络区域中，必然有结点个数不是 2的幂次的区域。由此，利用上面给出的经典对称gossip算法存在的充分必要条件，他们建立了量子gossip算法不可能性定理：对由任意n个量子比特组成的量子网络，有限时间收敛的gossip算法都不可能存在。下图给出了一个 3 量子比特的gossip算法等价的 64结点的分区块的经典对称gossip网络。

与本成果相关的论文： 

[1] Shi, G., Li, B., Johansson, M., & Johansson, K. H. (2016). Finite-time convergent gossiping. IEEE/ACM Transactions on Networking, 24(5), 2782-2794.

李博        libo@amss.ac.cn