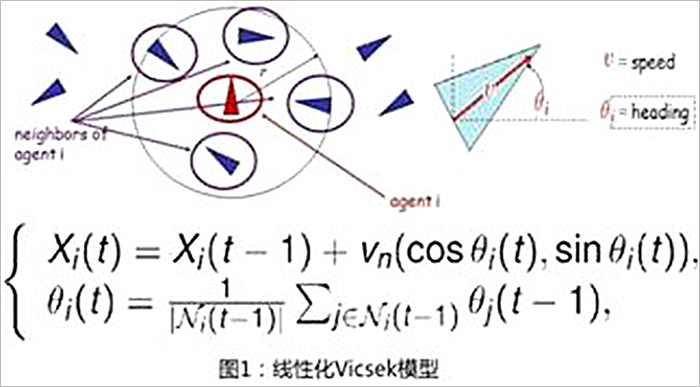
Vicsek模型同步条件属于多自主体系统理论研究的重要问题，在数学上，也有公认的难度。目前，大部分的相关理论研究需要强加一些不太合理的假设，例如闭环邻居关系图的联合连通性假设等，而我们是在一个更加自然和合理的理论框架-随机框架下进行研究。在随机框架下，G.G.Tang，Z.X.Liu和L.Guo等人有了重要进展，然而有一个悬而未决的问题是：系统能同步的最小交互半径是多少？我们利用渗流理论对随机几何图所对应平均矩阵的本质谱半径给出了一个充分必要条件，得到了线性化Vicsek模型同步条件的一个关于交互半径的临界结果：当个体间的交互半径高于临界连通半径时，如果速度满足一定条件，那么系统渐近以概率1对任意初始角度都同步；当交互半径低于临界连通半径时，对任意大的速度，系统都渐近以概率1存在某些初始角度使得最终不同步。因此在某种程度上解决了随机框架下Vicsek模型同步充分条件中交互半径的下限问题。

渗流理论是统计物理与概率论交叉的一门学科，也是现代概率论的一个重要分支。随机几何图理论是渗流理论的一个分支，它非常贴近于某些实际网络如无线传感器网络，生物网络等，越来越引起重视和关注。大连通分支性质属于随机几何图理论核心研究问题，它也与无线传感器网络拓扑控制等问题密切相关。我们证明了随机几何图或离散渗流大连通分支的阶或连通分支数目的期望以负指数的速度趋于一个多项式，并且，根据中心极限定理对这些随机变量的渐近大小作了精细刻画。该结果还能扩展到SIR模型最终感染人数等问题。这些结果是对Kensten、Penrose等人工作的本质改进。

在群体行为和多个体智能系统的研究中，邻居是个重要的概念。在现有的大部分模型中，个体的邻居由几何距离决定。但是最近，一些欧洲生物学家发现，鸟群中的邻居关系是由拓扑距离而非几何距离决定的，即，个体i的邻居是离i最近的k个个体, 其中k是参数。我们将这样邻居关系（简称“k个最近邻居规则”）引入到研究广泛的Vicsek模型中，研究在新的邻域定义下，“趋同”的局部信息交互规则是否可以引起宏观相变。我们证明了在大群体和随机框架下，当邻居个数k和个体的速度v满足一定条件时，系统可以产生同步行为。 特别的，当个体的邻居数目k与与群体数目n成比例时，对于任意的速度v，当n充分大时，系统都可以同步。

与本成果相关的论文：

[1] Ge Chen, Zhixin Liu and Lei Guo. “The smallest possible interaction radius for flock synchronization”. SIAM Journal on Control and Optimization, Vol 50, pp.1950-1970, 2012.

[2] Ge Chen, Changlong Yao and Tiande Guo. “The asymptotic size of the largest component in random geometric graphs with some applications”. To appear in Advances in Applied Probability, Vol 46(2), June 2014.

[3] Chen Chen, Ge Chen and Lei Guo. "Consensus of flocks under M-nearest-neighbor rules". Accepted by Journal of Systems Science and Complexity.

陈鸽          chenge@amss.ac.cn