在数字化设计与制造中，CAM（计算机辅助制造）是非常重要的一部分。对于建模之后的自由曲面，需要通过CAM规划刀具路径以及刀轴方向，然后生成数控机床可以识别的加工指令。对于给定的自由曲面，如何规划刀具路径是重要而有意义的问题。在数控加工中，基于三角网格的刀位点路径规划作为CAM中的重要组成部分，一直是国内外学者们的研究焦点。刀位点的路径规划可以归结为拓扑形式和参数形式。两种形式生成的路径轨迹大致可以分为以下几种情况：

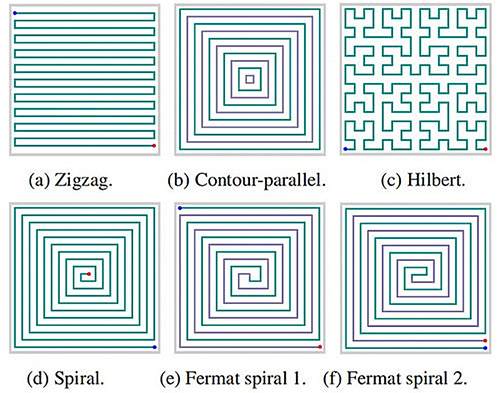
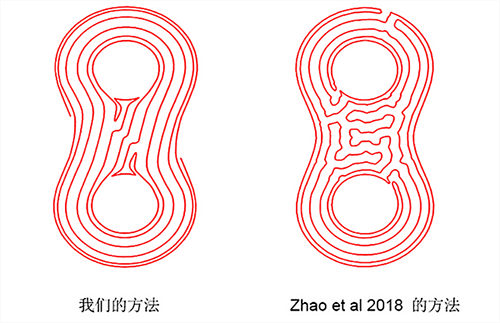
其中，Fermat spiral（费马螺旋线）具有显著优势，首先其转折角较少，而且可以一次加工成型，无需频繁抬刀。将待加工曲面上各个位置的Fermat spirals相连构成一条唯一的刀位点路径轨迹，我们称其为connected Fermat spirals（CFS）。在以前的工作中，zhao et al[ACM Trans. Graph 2016,2018]对CFS进行了深入的研究，设计了基于CFS的刀具路径规划方法。但是他的工作依然存在问题(如下图所示)：他们通过随机撒点并通过解优化问题来得到最终路径，使得路径迂回曲折，存在过多的弯折，不利于高速加工；在生成Fermat spiral的时候没有考虑动力学约束, 生成的路径过于曲折，会显著影响后续的加工速度。基于以上两个问题，袁春明等提出改进型的基于等残高方法的connected Fermat spirals。首先生成填充整个曲面的偏置曲线：使用搜索算法生成满足残高约束的测地线距离的偏置(offset)线。从而在满足残高约束的前提下避免太多的弯折，如图所示：

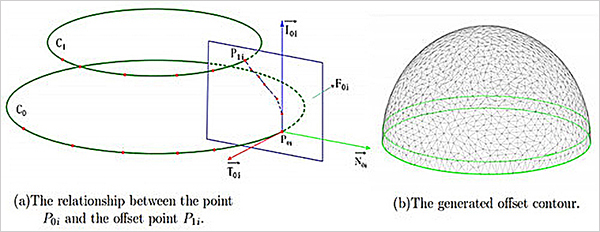
对于偏置曲线会发生自交( self-intersection)的现象，采用一种自适应调整局部曲线的方法来避免残高超界。最后根据动力学约束对Fermat spirals 进行合适的转接，从而得到光滑的刀具路径，利于高速加工。

实验结果表明，我们的方法与原有方法比较，整体上具有更好的光滑性和易加工性，检验表明，我们最终生成的刀具路径严格满足残高约束。我们对我们的方法和已有方法(Zhao et al)进行了仿真测试，实验结果表明，与原有方法相比，根据机床参数的不同，我们的算法的加工效率提高2倍左右。

 袁春明          cmyuan@mmrc.iss.ac.cn