有效性(Effectiveness)与可定义性(Definability)分别是计算复杂性与数理逻辑研究中的基本问题。有效性研究旨在给出相应问题的一致上界，保证算法设计的终止性，并在分析算法的计算复杂度中有重要应用。可定义性研究可被应用于解决一些困难的存在性问题，例如微分周簇的存在性、微分Galois理论中的逆问题等。2020年度我们在计算微分差分代数中的有效性与可定义性问题研究中取得如下重要进展：

(1) 解决了有效微分-差分Hilbert零点定理

相容性判定是方程求解的基本问题。对于代数方程组，Hilbert零点定理断言方程组无解当且仅当1可以表示成这些方程的多项式系数线性组合。有效Hilbert零点定理(Effective Nullstellensatz)问题即是要给出表达式中待定多项式系数的一致次数上界(仅依赖于系统的次数与变量个数)，将代数方程组的相容性判定问题转化为线性方程组的求解问题。该问题的最优上界分别由Brownawell (Ann.Math., 1987), Kollar (J. AMS,1988), Jelonek (Invent.Math., 2005)等给出。对于代数微分或差分方程组，方程组在微分域或差分域中无解当且仅当其若干阶算子延拓所得代数方程组无解。有效微分(差分)Hilbert零点定理则是要给出算子延拓阶数的一致上界，将微分(差分)方程组的相容性判定问题归约到代数方程组的相容性判定问题。目前，Gustavson等(Adv. Math.,2016), Leon-Sanchez等(J. Algebra,2018)给出了有效微分Hilbert零点定理的一致上界；Ovchinnikov等(J.EMS, 2020)给出了有效差分 Hilbert 零点定理的一个由递归函数定义的上界 。

代数微分-差分方程(即时滞微分方程)及其序列解在生物学、人口动力学等领域有广泛应用。一个重要的未解决问题是微分-差分方程的相容性判定问题：是否存在一个算法来判定任意给定的微分-差分方程组有无序列解？2007年，数理逻辑专家Hrushovski (国际数学家大会1小时报告人)-Point证明了序列环作为微分-差分环的理论是不可判定的，由于序列环不具有量词可消去的性质，通过逻辑方法不能导出相容性判定问题的算法。我们近期的工作解决了有效微分-差分Hilbert零点定理问题：给出了一个仅依赖于系统的阶数、次数以及变元个数的一致可计算上界 B, 证明了任意给定的微分-差分混合方程系统 P 有序列解当且仅当由 P 及 P 的不超过 B 阶的算子延拓方程构成的代数方程组有解；另外，证明了复系数的微分-差分方程系统存在序列解当且仅当该系统在亚纯函数的芽环中有解。该项成果通过代数方法给出了微分-差分方程组相容性判定问题的一个有效算法。相关论文[1]发表在美国数学会会刊 Trans. Amer. Math. Soc..

(2) 证明了微分维数多项式的可定义性

在微分闭域的模型论研究中，微分指标(秩)是否具有可定义性(definable in families)是微分代数学家与模型论专家的研究热点。例如, Pillay、Nagloo证明了Morley秩、Lascar秩与微分Krull维数都不具有可定义性；而微分簇(即代数微分方程组的解集)的不可约性是否具有可定义性与微分代数中经典的Ritt公开问题等价。微分维数多项式,也称Kolchin多项式，是微分簇的一个非常重要的双有理不变量。在常微分情形，Freitag等(2017)证明了微分维数与阶数的可定义性，从而证明了常微分情形微分维数多项式的可定义性。我们近期的工作给出了Hilbert-Kolchin正则度的有效上界，证明了偏微分簇的微分维数多项式具有可定义性。具体来说，对于任意的一族含参微分簇，考虑微分维数多项式等于某个整值多项式的微分簇的集合，我们证明了相应参数集是一个微分可构造集，并证明了微分簇的弱不可约性也具有可定义性。相关论文[2]发表在 Proc. Amer. Math. Soc..

(3) 发展了偏微分方程的generic相交理论与偏微分周形式理论

周形式是代数几何的基本概念,被用于超越数论、消去理论等领域取得了一些深刻结果。周形式理论是由周炜良与van der Warden在1937年建立的。通过周形式,周给出了代数簇的周坐标表示；并证明了所有具有固定维数与次数的代数闭链的周坐标的集合是高维射影空间中的一个代数簇，称为周簇。周簇是代数簇的一类非常重要的模空间.

微分代数几何的基本研究对象是微分簇(包括常微分簇与偏微分簇)。研究微分簇的坐标表示，发展微分周形式理论以及微分簇的模空间理论，是推动微分代数几何发展的重要研究问题。在常微分情形，Gao等(2013)证明了generic微分相交定理，以此为基础，建立了常微分簇的微分周形式理论，证明了一类微分闭链的微分周簇的存在性；Freitag等(2017)应用模型论证明了一般情形微分周簇的存在性。偏微分情形的微分周形式理论一直未得到发展，其本质困难在于：在偏微分情形，余维数为1的偏微分簇可能不是一个超曲面的主分支。我们近期发展了偏微分方程的generic相交理论，证明了拟-generic偏微分相交定理，即一个微分维数大于1的不可约偏微分簇V与一个阶数为s的拟-generic偏微分超曲面的交是一个不可约偏微分簇，其微分维数多项式为: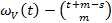；给出了偏微分周形式存在的充要条件，对于微分维数多项式为(d+1)的偏微分簇定义了偏微分周形式，证明了偏微分周形式的基本性质，特别引入了偏微分周坐标与偏微分次数的概念；并应用可定义性研究证明了一类偏微分周簇的存在性，即偏微分周坐标满足微分方程。相关论文[3]发表在Communications in Algebra.

(4) 微分曲线的有理参数化

代数曲线的有理参数化是计算代数几何的一个核心研究问题，目前理论与算法已经非常成熟，并在计算机辅助几何设计、生物模型、纠错码等领域具有广泛应用。微分簇的有理参数化问题是微分代数几何领域的重要问题。作为零维一阶情形Poincare问题的推广，该问题对揭示微分曲线的双有理等价分类具有重要意义。对于一维空间中的零维微分簇，Feng-Gao(2006)的工作首次给出了单变量常微分方程存在有理通解的充要条件，并在一阶自治情形给出了计算有理通解的多项式算法，是研究微分有理参数化问题的开端；Winkler等陆续将该方法扩展到研究一阶非自治含参常微分方程、高阶常微分方程以及偏微分方程的有理通解。但是，对于正维数的微分簇，如微分曲线，相应的微分有理参数化问题尚未得到研究。

我们研究了微分曲线的有理参数化问题，取得如下进展: a)对微分有理曲线引入了恰当有理参数化表示，研究了恰当微分有理参数化的基本性质，特别地，给出了恰当参数化表示的阶数与隐式化方程的阶数之间的对应关系，证明了恰当参数化在M?bius变换下的唯一性；b) 对于线性微分有理参数化表示，基于微分结式，给出了判定其恰当化的充要条件，并给出了隐式化的高效算法；c) 对于线性微分曲线，给出了其存在微分有理参数表示的判定条件，即证明了线性微分曲线是有理的当且仅当相应线性微分算子的最大左公因子为1；基于线性微分算子的扩展欧几里德算法，设计了一个高效算法用于判定线性微分曲线是否可有理参数化，并计算微分有理曲线的恰当参数化表示。相关论文[4]被J. Symb. Comput.接收并在线发表。

[1] W. Li, A. Ovchinnikov, G. Pogudin, and T. Scanlon. Elimination of unknowns for systems of algebraic differential-difference equations. Trans. Amer. Math. Soc., electronically published on October 14, 2020. (https://doi.org/10.1090/tran/8219)

[2] J. Freitag, O. Leon-Sanchez, W. Li. Effective definability of Kolchin polynomials. Proc. Amer. Math. Soc., 148(4), 1455–1466, 2020.

[3] W. Li. Partial differential Chow forms and a type of partial differential Chow varieties. Communications in Algebra, 48(8), 3342-3371, 2020.

[4] L. Fu and W. Li. Differential unirational curves and differential rational parametric representations. Accepted for publication by Journal of Symbolic Computation, 2020. (https://doi.org/10.1016/j.jsc.2020.08.008.)

 李伟          liwei@mmrc.iss.ac.cn